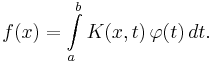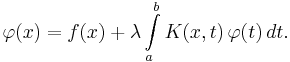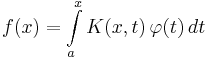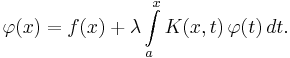Integral equation

In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way. See, for example, Maxwell's equations.

1 Overview
2 Classification
3 Integral equations as a generalization of eigenvalue equations
4 References
5 See also
6 External links

Overview

The most basic type of integral equation is a Fredholm equation of the first type:

$f(x) = \int \limits_a^b K(x,t)\,\varphi(t)\,dt.$

The notation follows Arfken. Here φ; is an unknown function, f is a known function, and K is another known function of two variables, often called the kernel function. Note that the limits of integration are constant; this is what characterizes a Fredholm equation.

If the unknown function occurs both inside and outside of the integral, it is known as a Fredholm equation of the second type:

$\varphi(x) = f(x)%2B \lambda \int \limits_a^b K(x,t)\,\varphi(t)\,dt.$

The parameter λ is an unknown factor, which plays the same role as the eigenvalue in linear algebra.

If one limit of integration is variable, it is called a Volterra equation. Thus Volterra equations of the first and second types, respectively, would appear as:

$f(x) = \int \limits_a^x K(x,t)\,\varphi(t)\,dt$

$\varphi(x) = f(x) %2B \lambda \int \limits_a^x K(x,t)\,\varphi(t)\,dt.$

In all of the above, if the known function f is identically zero, it is called a homogeneous integral equation. If f is nonzero, it is called an inhomogeneous integral equation. φ

Classification

Integral equations are classified according to three different dichotomies, creating eight different kinds:

Limits of integration: both fixed: Fredholm equation; one variable: Volterra equation
Placement of unknown function: only inside integral: first kind; both inside and outside integral: second kind
Nature of known function f: identically zero: homogeneous; not identically zero: inhomogeneous

Integral equations are important in many applications. Problems in which integral equations are encountered include radiative energy transfer and the oscillation of a string, membrane, or axle. Oscillation problems may also be solved as differential equations.

Both Fredholm and Volterra equations are linear integral equations, due to the linear behaviour of φ(x) under the integral. A nonlinear Volterra integral equation has the general form:

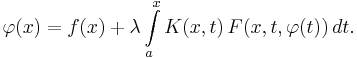$\varphi(x) = f(x) %2B \lambda \int \limits_a^x K(x,t)\,F(x, t, \varphi(t))\,dt.$ ,

where F is a known function.

Integral equations as a generalization of eigenvalue equations

Certain homogeneous linear integral equations can be viewed as the continuum limit of eigenvalue equations. Using index notation, an eigenvalue equation can be written as

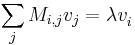$\sum _j M_{i,j} v_j = \lambda v_i^{}$ ,

where 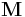$\mathbf{M}$ is a matrix, 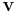$\mathbf{v}$ is one of its eigenvectors, and $\lambda$ is the associated eigenvalue.

Taking the continuum limit, by replacing the discrete indices $i$ and $j$ with continuous variables $x$ and $y$ , gives

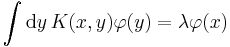$\int \mathrm{d}y\, K(x,y)\varphi(y) = \lambda \varphi(x)$ ,

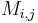where the sum over $j$ has been replaced by an integral over $y$ and the matrix $M_{i,j}$ and vector 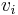$v_i$ have been replaced by the 'kernel' 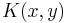$K(x,y)$ and the eigenfunction 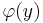$\varphi(y)$ . (The limits on the integral are fixed, analogously to the limits on the sum over $j$ .) This gives a linear homogeneous Fredholm equation of the second type.

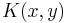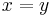In general, $K(x,y)$ can be a distribution, rather than a function in the strict sense. If the distribution $K$ has support only at the point $x=y$ , then the integral equation reduces to a differential eigenfunction equation.

References

George Arfken and Hans Weber. Mathematical Methods for Physicists. Harcourt/Academic Press, 2000.
Andrei D. Polyanin and Alexander V. Manzhirov Handbook of Integral Equations. CRC Press, Boca Raton, 1998. ISBN 0-8493-2876-4.
E. T. Whittaker and G. N. Watson. A Course of Modern Analysis Cambridge Mathematical Library.
M. Krasnov, A. Kiselev, G. Makarenko, Problems and Exercises in Integral Equations, Mir Publishers, Moscow, 1971
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Chapter 19. Integral Equations and Inverse Theory". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=986.

External links

Integral Equations: Exact Solutions at EqWorld: The World of Mathematical Equations.
Integral Equations: Index at EqWorld: The World of Mathematical Equations.